Résumé
La logique tétravalente constitue sans aucun doute un pas à franchir dans notre compréhension de l'univers. Elle est utilisée sur Oummo conjointement avec le concept de Ibodzo-Ou. Ses domaines d'application sont la cosmologie, la biologie, la psychologie, la philosophie, etc.
Dans cette première partie nous allons tenter de répertorier les principes qui permettent d'aborder la logique tétravalente en se plaçant dans le cadre des connaissances acquises dans le domaine de la logique. Ces domaines vont des mathématiques à la philosophie en passant par la linguistique. Cela nous permettra d'avoir une vue plongeante sur les propriétés de la logique tétravalente.
Dans les articles suivants nous allons tenter d'illustrer quelques principes des Ibodzo-Ou, revenir sur la cosmogonie Oummaine soutenue par la logique tétravalente en évoquant l'Aïoodi (la réalité) et l'Aïoodii ("la vérité") et enfin on s'amusera à échafauder des exercices pour tenter d'apprivoiser la logique tétravalente, dessiner des résultats désirés, et tenter de formaliser des applications.
Il est clair que cet article relève d'un niveau scientifique que nous n'avons pas du tout, qui est amplement interdisciplinaire, donc n'hésitez pas à apporter les corrections qui vous semblent déterminantes.
Introduction
Pour donner un aperçu simplifié, est appelée "logique binaire" le système de raisonnement basé sur le principe aristotélicien selon lequel ce qui est vrai, n'est pas faux, par déduction simple et directe. En logique "binaire" la formalisation d'une preuve n'existe pas : la proposition "tous les arbres sont verts" ne pourra être vérifiée que de façon empirique. C'est un grave écueil qui vaut bien des tergiversations inutiles dans la vie courante.
Cela n'empêche pas que les mathématiques "binaires" soient considérées comme les plus fiables, puisqu'elles permettent d'échafauder un grand nombre de systèmes et de conventions pour la résolution de problèmes complexes, qui font appel au raisonnement pour aboutir à des réponses formelles.
Le terme de "logique binaire" se réfère à la logique classique (LC) et a pour conséquence de marquer une distinction de classe. Car dès lors qu'on s'attache à analyser des propositions dialectiques, la logique mathématique, sur laquelle on se précipite, doit d'abord passer par le filtre d'un entendement linguistique, qui lui aussi tend à se doter d'un formalisme.
Il en résulte que les mathématiques ne sont plus le point de départ de l'analyse, mais un outil d'analyse, dont l'interprétation est ensuite laissée à l'utilisateur. En dialectique, une proposition est difficilement "vraie dans l'absolu". Même "cette pomme est rouge" pourra invoquer de grandes notions sur ce qu'est en réalité la couleur rouge.
L'intérêt de la logique tétravalente est qu'elle emploie des procédés qui sont passablement issus d'une synthèse des logiques existantes, si bien que cela ne fera pas de mal de tenter de les passer en revue, en glanant les notions qui permettent d'enrichir notre compréhension des termes qu'elle utilise.
Il sera ensuite question d'établir un cadre de validité pour la logique tétravalente, ce qui sera l'occasion de créer des distinctions très intéressantes.
Mais d'abord, avant de commencer, reprenons tout depuis le début...
Une brève histoire de la logique
Dans cette partie nous n'avons pas la prétention d'être exhaustifs et assez précis, il ne s'agit que d'avoir un aperçu des cheminements qui peuvent conduire à l'élaboration d'une logique tétravalente. Tout ce qui est développé ne sera pas nécessairement utile, mais permettra d'avoir une vue d'ensemble sur le choix des axiomatiques qui font la logique. Par soucis de vulgarisation, certaines explications sont approximées.
Les mathématiques permettent de construire des outillages qui rendent exploitables les questions complexes, mais ce n'est qu'au siècle dernier que le pont a été jeté entre les mathématiques et la logique à proprement parler. Avant cela, la logique des mathématiques était simplement supposée vraie, jusqu'à ce que les philosophes se soient interrogés sur ce qui fondait les mathématiques.
Cantor, le premier, a créé la branche des mathématiques dénommée la théorie des ensembles, permettant d'isoler des suites de nombres rationnels en groupes distincts, et d'envisager autant de suites infinies que de groupes, ce qui peut s'illustrer par de simples axes orthonormés. Et déjà, on peut reconnaître un formalisme rencontré dans la Nr20 :
si on prend l'ensemble 𝒳 = {1/𝓃 ∣ 𝓃 ∈ ℕ∗} ∪ {0} alors chaque nombre 1/𝓃 est isolé dans 𝒳 si bien que 𝒳′ est simplement {0}. Ce dernier ensemble peut à son tour se dériver et son dérivé est l'ensemble vide.
Où :
- "|" se lit : "tel que"
- "∈" : "appartient à"
- "∩" : "intersection"
Les axiomes de Peano
Ce formalisme est fondateur des systèmes logiques. Il s'agit de l'arithmétique fondée sur les axiomes de Peano, qui n'accepte que les symboles "∃" (il existe), "∀" (pour tout), "¬" (n'est pas), → (implique), "ᐱ" (et), "ᐯ" (ou), et S (suivant dans l'ordre des nombres). Et c'est tout, rien d'autre n'est autorisé, hormis les parenthèses pour ordonner les calculs. Toutes les mathématiques doivent être démontrables par des axiomes de Peano, sinon elles sont jugées fausses.
Les axiomes sont peu nombreux, et très basiques, tels que, le premier et le deuxième :
∀𝓍 ¬(S𝓍=0)Pour tout 𝓍 il est faux de dire que son successeur est 0.
∀𝓍∃𝓎 ¬(𝓍=0) → (S𝓎=𝓍)
Pour tout 𝓍 il existe un 𝓎 tel qu'il est faux de dire que si 𝓍=0, alors le successeur de 𝓎=𝓍.
Il faut noter que dans la logique de Péano, dont les axiomes sont un complément, il s'existe pas de signe "=" (égal) ou tout autre opérateur. Ces opérateurs doivent être construits selon une forme logique, pour être utilisés ensuite en référence à ces démonstrations. Ainsi les opérateurs, qu'on appellera ensuite des connecteurs (parce qu'on pourra leur assigner différentes significations) doivent être eux-mêmes justifiés. On ne peut pas confier au simple entendement le soin de s'imaginer ce que sont les choses qu'on utilise dans une arithmétique. Pourtant, on ne cesse de découvrir que c'est qui est fait, le plus souvent, par mégarde et par habitude.
Ainsi le signe "=" est un axiome de transitivité de l'égalité, qui implique que l'égalité est valable dans les deux sens. La transitivité est ce qui rend possible le syllogisme, qui est la démonstration logique la plus simple possible, selon laquelle si a=b et b=c alors a=c.
Un des axiomes de Peano est plus important que tous les autres et permet de traiter les nombres infinis, afin d'écrire "⋯", c'est le schéma d'axiomes de récurrence, qui dit en gros que ce qui est valable pour un calcul, le devient pour les autres qui sont similaires. Il faut noter enfin que si cette logique des prédicats est de premier ordre, le schéma de récurrence est du second ordre.
La théorie des ensembles
La théorie des ensembles s'est ensuite affinée pour mieux les définir (car à leur tour leur définition était confiée au "bon sens"), en introduisant le concept d'axiomes (c'est à dire "de nouvelles instances du principe de compréhension générale"). Les axiomes originaux de Zermelo (paires, réunions, parties d'ensembles) ont été complétés par l'axiome de remplacement de Fraenkel, donnant la théorie "ZF", puis complétée ensuite par Skolem qui a introduit l'axiome du choix (C), laissant libre la définition du type d'ensemble, pour donner lieu à la théorie "ZFC", fondement de la logique mathématique moderne, dite "logique classique" (LC).
L'intérêt de l'axiome du choix est de certifier la taille des infinis, hypothèse qui permet aux logiques du premier ordre d'accepter des modèles, afin de correspondre à la nécessité de complétude d'une logique (qu'on verra ensuite).
C'est toujours à ces fondements que feront référence la fabrication des modèles sur lesquels se basent les différents systèmes logiques. Si la théorie ZF utilise des axiomes solides, la théorie ZFC permet de construire des infinis.
Finalement, et historiquement, c'est ainsi qu'a été introduit la notion de prédicats, définissant le contexte de validité logique, ce qui a ensuite donné lieu à la logique intuitionniste, sur laquelle on va revenir.
Le schéma de compréhension
Le schéma d' axiome de compréhension de Zermelo est un principe faisant que les propriétés peuvent définir leurs propres axiomes, qui peuvent être librement ceux de la théorie Z, ZF ou ZFC. Il en découle la formalisation de l'ensemble vide :
∅ = { x ∈ A | x ≠ x }
Ainsi, Zermelo introduit le principe du terme-tiers : "Pour tout ensemble A il existe un ensemble qui n'appartient pas à A". Finalement ce "schéma de compréhension" qui revient à peu près à pouvoir faire ce qu'on veut puisque chaque propriété définit son propre groupe, a fait remarquer à Bertrand Russell une contradiction native, définie par la suite comme une véritable antinomie, en demandant si un ensemble, qui contient des objets qui peuvent être des ensembles, peut s'appartenir à lui-même, ce qu'il exprime par l'adage : "un barbier ne rase que les hommes qui ne se rasent pas eux-mêmes : peut-il se raser ?". Soit, formellement :
Un modèle de la théorie ZFC est non-vide, donc il existe un ensemble tel que :∅ = {𝓍 ∈ A | 𝓍 ∉ 𝓍}
où 𝓍 ne dépend pas de A. Dans le schéma de compréhension non restreint, toute propriété définit un ensemble {𝓍 | P𝓍}, d'où le paradoxe de Russell :
𝓎 = {𝓍 | 𝓍 ∉ 𝓍}
où 𝓍 ne s'appartient pas à lui-même...
Il résout (ou pense résoudre) cette énigme en introduisant, dans Principia Mathematica (1910), le principe de hiérarchisation des types d'ensembles, la théorie des types, qui ouvrit la voie à l'informatique, et sera l'objet, cent ans plus tard, d'une nouvelle refondation des mathématiques sur la base des types homotopiques (on y reviendra).
Note en passant : Le principe d'objets qui contiennent des ensembles évoque le DOM. Ce dernier est constitué de nœuds qui sont des objets (passablement) vides, dans lesquels se trouvent les nœuds des contenus, en html. Ou plus simplement cela évoque aussi le JSON, où deux types de données, alphanumériques et numériques, sont représentés par des parenthèses associées, par exemple dans : {"a":[1,2,3]}. Il n'est pas possible par exemple d'écrire : "[1,2,3:{"a":[1,2,3]}]" (de mettre un tableau où on attend un intervalle) à cause de la hiérarchisation des types.
Il est toutefois un peu décevant que la résolution du paradoxe consiste seulement à ajouter un axiome à une théorie qui reste encore perfectible (en toute logique). Ainsi il ne peut y avoir d'ensemble de tous les ensembles sans nécessairement créer une classe qui lui est propre.
Note en passant : Tout ceci ressemble un peu à du Frankenstein d'un lecteur de Wikipedia, je m'en excuse, mais cette remarque permet d'illustrer comment la définition de soi-même peut conduire à la création de nouvelles catégories :)
C'est intéressant parce que progressivement les chercheurs finissent par tisser des relations entre les ensembles et formaliser des règles de ces relations, ce qui est un prémisse des systèmes logiques modernes.
La publication de la résolution du paradoxe de Russell dans Principia Mathematica coupe le sifflet à Frege qui pensait fonder les mathématiques sur des bases purement logiques (ce qui lui valu d'arrêter les rotatives de l'imprimeur pour y ajouter une mention "désolé, je me suis planté"). Et pourtant, ce deuxième ouvrage "fondateur", qui a demandé dix ans de travail pour être publié et n'a intéressé qu'une toute petite poignée de spécialistes, n'a jamais vraiment atteint ce même but qu'il s'était fixé, "trouver des bases logiques". En revanche il aura développé tous les outils qui permettront de prouver sa réfutation, ce que Gödel s'empressera de faire.
L'histoire a trop peu prêté attention au co-auteur de cet ouvrage extraordinairement complexe (où il faut attendre la page 86 du second tome pour réussir à prouver que 1+1=2, "ce qui peut servir", disent-ils en s'amusant), Ernest Whitehead. Illustre philosophe et ancien professeur de Bertrand Russell, il a certainement été un facteur important dans la conduite d'une logique impliquant le terme-tiers. On y reviendra
La logique intuitionniste
Consécutivement, apparaît la logique dite "intuitionniste" (LI), qui se fonde, elle, sur le non-rejet du tiers-exclu, ce qui n'est pas du goût des tenants de la logique classique (LC), mais que son auteur, Jan Brouwer, juge "plus intuitive", en raison du fait que pour lui, "la logique doit être accessible à la compréhension". De ce fait, la logique intuitionniste rejette aussi le raisonnement par l'absurde (souvent efficace en LC), et fonde sa logique sur le constructivisme (l'inverse ce de que laisse supposer le terme "intuitionnisme").
Bien que n'arrivant à rien prouver de plus que ce que la logique classique permet de prouver, elle apporte, elle aussi, un nouvel outillage fait de "constructeurs", qui a une forte résonance en informatique. Elle introduit le terme de "prouvabilité" en lieu et place du terme de "vérité", le terme de "⊥" ("Absurde") qui se dérive en "¬" (inexistence), et requalifie les opérateurs comme des connecteurs qui peuvent chacun avoir leurs propres règles. C'est un peu comme si le "C" du ZFC (le choix) s'appliquait désormais aussi aux opérateurs, qui deviennent des algorithmes.
Γ ⊢ φ"De l'ensemble des propositions Γ (Gamma), on en déduit (⊢) la proposition φ (Phi)"
Brouwer juge que le tiers exclu, un principe logique qui affirme qu'une proposition est soit vraie soit fausse, s'il repose sur une intuition solide quand on manipule le fini, ne peut être un principe du raisonnement, dès que l'on manipule l'infini. Une preuve d'existence doit être effective. Il ne suffit pas, pour montrer telle proposition, de montrer que sa négation entraînerait une contradiction. Cette position, cohérente sur le plan des idées, et qui séduit des mathématiciens de valeur - outre Brouwer lui-même, Hermann Weyl pendant un temps - a pour principal défaut, de remettre en cause des pans entiers des mathématiques (source wikipedia).
Note de compréhension : Dans ce passage de wikipedia, on comprend que l'intégration du tiers-exclu est ce qui force la bivalence, tandis que son rejet, est ce qui l'en empêche (le rejet du tiers-exclu est une double-négation). De plus il crée une distinction entre la manipulation du fini et celle de l'infini, qui va s'avérer très pertinente pour nous par la suite. C'est même extraordinairement lucide.
Cette phrase désigne le tiers dialectique (non-exlu) comme un terme médian ou un terme tiers, c'est à dire une reformulation ou un ajout. L'exclusion de ce tiers n'est pas "formellement" acceptée. C'est à dire qu'elle l'est principalement, ce qui, on le comprend, signifie que le tiers-exclu est principalement accepté, mais pas formellement. Mais surtout, l'acceptation du tiers-exclu signifie un formalisme de la logique classique, principalement.
Une autre propriété remarquable de la logique intuitionniste, dite aussi "constructiviste", outre le fait que les connecteurs soient eux-mêmes typés, est d'avoir créé un distinguo entre le "vrai" et le "prouvable" (et le "faux" et le "non-prouvable"). De ce fait, la double-négation ne peut plus être une démonstration de l'affirmation.
L'intuitionnisme est défendu de manière paradigmatique par Brouwer : les mathématiques ont un fondement intuitif, c'est-à-dire que tous les objets des mathématiques sont des constructions de l'esprit humain. Selon la conception intuitionniste un nombre réel peut être représenté comme une suite infinie de décimales à condition de disposer d'un algorithme qui peut calculer chacune de ces décimales. Cette position a des conséquences importantes notamment sur le plan logique. En logique intuitionniste, on ne peut pas éliminer la double négation (alors que cela est possible en logique classique) : « non non p » ne se réduit pas à « p » ; sinon on pourrait démontrer l'existence d'objets sans pour autant construire ceux-ci. Il s'ensuit que « non p ou p » n'est pas un théorème. Brouwer concevait l'intuitionnisme comme un positionnement philosophique sur les mathématiques et a accueilli avec scepticisme sa formalisation donnée ultérieurement par Arend Heyting (source wikipedia).
La logique intuitionniste a encore de beaux jours devant elle et a donné lieu à une variante moderne dite "homotopique" très élégante, mais qui n'arrive pas à rivaliser avec la logique classique constituant la base la plus solide pour les calculs déterministes. La recherche sur les fondements des mathématiques est toujours d'actualité. On entend souvent les chercheurs affirmer que "l'univers est une machine de Turing", ou encore "l'univers est un algorithme" (d'après les chercheurs de chez Google), mais cette assertion ne prend pas en compte les développements sur les logiques qui ne se briment pas elles-mêmes en acceptant le tiers-exclu, et ont encore un grand potentiel évolutif.
Il subsiste cependant plusieurs problèmes qui hantent la logique classique, comme par exemple le fait que la sommation des nombres de zéro à l'infini soit égal à -1/12... voir youtube ). Ou encore, de manière encore plus triviale, le fait 1/3*3≠1 (=0.9999...).
Cela démontre l'incroyable ténacité de la psychologie à "croire aveuglément" ce qu'elle obtient par le calcul formel alors que c'est objectivement faux. 0.333 n'est pas "une" réalité. Peut-être qu'il faudrait introduire un terme de virgule après l'infini, comme 0.333.⅓, ou encore de virgule de virgules : 3.3.3.3.3...3.3.3...3.3. etc. Qu'on pourrait écrire 3...3, tout simplement. C'est juste une idée en passant, mais de toutes manières c'est absurde et on comprendra mieux cela dans les articles suivants.
C'est Kurt Gödel qui a donné ce doux nom de "logique intuitionniste" au formalisme de Brouwer, probablement parce qu'il s'en sentait un peu le père spirituel. En effet le théorème de complétude permet de dresser un pont entre sémantique et mathématiques, dans la mesure où tout énoncé qui s'exprime par des prédicats (algébriques du premier ordre), est vrai s'il est démontrable. Un énoncé devient "une loi" s'il est valable pour tous les prédicats du modèle qui a été choisi.
La théorie des modèles
La théorie des modèles traite de la construction et de la classification des structures. Elle permet d'interpréter les structures syntaxiques dans les ensembles mathématiques de façon à leur associer des concepts de nature sémantique.
Théorème de complétude : "Toute théorie non-contradictoire possède un modèle" (comme par exemple l'arithmétique de Péano se fonde sur un schéma d'axiomes). Les modèles supportent ainsi toutes les logiques "L" (en disant cela Gödel a le génie de supposer des logiques indéfinies). Ils permettent de satisfaire ou de falsifier toute formule, et de prouver qu'une théorie ou un système d'axiome est non-contradictoire. L'application des modèles montre l'indépendance des axiomes entre eux, ce qui est une exigence de la logique. Elle permet d'établir, ce qui est aussi une exigence élémentaire, la non-contradiction du système axiomatique avec d'autres modèles. D'où principalement une de ses techniques qui consiste à "tester" le modèle avec un ensemble vide.
si ⊢p alors ⊨pSi P est démontrable alors P est une conséquence logique
Il en découle que l'ensemble des lois logiques (L) est indécidable, puisque l'ensemble des lois falsifiables, tout comme l'ensemble des lois vraies, est non-énumérable.
Le théorème d'incomplétude du même Gödel, va plus loin en affirmant que tout système logique (L) ne peut être infirmé ou confirmé à partir de ses propres axiomes (pourvu qu'ils soient cohérents), ce qui fit de lui une célébrité mondiale. Il poussa même le culot d'en faire la démonstration en utilisant les lois logiques développées par Russell et Whitehead, réduisant à néant leurs efforts pour fonder une logique mathématique. Par corollaire une théorie est cohérente s'il existe des énoncés qui n'y sont pas démontrables, comme le prouve 1=0, qui est nécessairement faux.
Si T est une théorie cohérente qui satisfait des hypothèses analogues, la cohérence de T, qui peut s'exprimer dans la théorie T, n'est pas démontrable dans T.
(Ce qui jette un pavé dans la mare)
Ainsi, il prouve de façon formelle, contrairement à ce que soutient la logique classique, que vérité et prouvabilité sont deux choses distinctes.
Note en passant : cela me rappelle une des premières enquêtes policières utilisant l'Adn, où le cheveu de l'accusé retrouvé sur la victime provenait finalement du fait qu'il passait pas là en voiture décapotable... La prouvabilité n'est pas la vérité.
Il en découle que si une théorie est prouvable par de simples principes arithmétiques, définir sa vérité nécessite des moyens qui lui sont extérieurs... tout en partant du principe que cette théorie est cohérente (ce qui reste aussi à prouver).
Note en passant : C'est très intéressant sur le plan philosophique parce que tout prémisse d'une théorie doit toujours être (et est toujours, hélas) considérée comme absolument vraie, ce qui conduit immanquablement à ne pas pouvoir comprendre la raison pour laquelle les conclusions sont fausses ou absurdes. Cela arrive très souvent dans la vie courante... Considérer ses prémisses comme absolument vraies empoisonne toute démonstration, et pourtant, elles ne le sont presque jamais. L'étude de la logique devrait vraiment être beaucoup plus promue pour populariser l'idée qu'il vaut toujours mieux réviser les prémisses des idées stressantes plutôt que de se disputer... qui revient à les admettre implicitement, et bêtement.
Note superfétatoire : Les prémisses restent toujours dans l'ombre des affirmations, et sont des constructions psychologiques par défaut, qui ne sont là que pour faire démarrer la réflexion. Un prémisse par défaut, par exemple, était le fait d'avoir considéré le virus Sars-nCoV-19 comme "statique dans le temps", ce qui est objectivement faux, mais n'a jamais été interrogé ou étudié, alors qu'il y avait tant à dire et à découvrir à ce sujet. (mise à jour) Et une fois qu'on a découvert des variants, on les a stigmatisés comme "des mutants" alors qu'il y en a des milliers, pour la simple raison que sa contagiosité augmente avec la baisse de sa virulence, avant que le virus ne redevienne inoffensif (ce qui suppose sa fabrication en laboratoire). Mais là encore, les détails de la bio-logique n'ont pas l'air d'intéresser grand monde...
Bref, c'est ainsi que Gödel a officiellement rendu inaccessible le but que s'était fixé Principia Mathématica, qui cherchait à fonder les mathématiques sur des bases logiques. Il a prouvé, pour le dire simplement, que les mathématiques étaient inconsistantes, ce terme étant la pire insulte pour un scientifique...
Mais cela n'a pas empêché, en l'absence d'un modèle alternatif plus "complet", de voir se développer l'énorme panoplie de solutions que nous exposons ici.
Note en passant : puisqu'il est publié au moment de la relecture de cet article, on peut conseiller cet article sur les dérives politiques qui découlent de mathématiques inconsistantes : De Russell et Hilbert à Wiener et Harari : les inquiétantes origines de la cybernétique et du transhumanisme
Le lambda-calcul (ou λ-calcul)
Ensuite, est apparue la logique de deuxième ordre, où l'on considère les fonctions et les prédicats comme des objets au même titre que les nombres. Rappelons-nous que le formalisme ZFC obligeait déjà à considérer les ensembles comme des objets, dont le typage était le principal problème. En lambda-calcul on peut doter un système formel d'un mécanisme de typage pour restreindre la nature des objets.
La thèse de Church érige une définition de la calculabilité selon laquelle tout traitement sémantique est réalisable par un processus physique ou mécanique, exprimé en un ensemble de règles de calcul. Ce à quoi Alan Turing ajoute la définition de la lambda-définissabilité, selon laquelle les instructions doivent être simples, leur nombre doit être fini, leur déroulement doit être possible à suivre par un humain, et ne nécessite pas l'intelligence humaine pour s'exécuter.
C'est ainsi qu'il a bâti la machine de Turing, une mécanique qui fait des opérations élémentaires, qui servent de fondement pour absolument n'importe quel calcul possible dans l'univers, et du coup, permet de réduire les mathématiques à une base logique irréductible, ce qui est un tour de force. Elle permet d'associer n'importe quelle instruction avec des paramètres et de garantir que n'importe quelle machine produira toujours le méme résultat, ce qui est nommé l'idempotence.
Un prédicat prend pour argument un ou plusieurs prédicats, ce qui est appelé le lamba-calcul, et permet d'obtenir des résultats de décidabilité du résultat. Il en résulte une théorie de la calculabilité et une théorie de la démonstration, qui est une discipline mathématique proposée au début du siècle par David Hilbert (un des plus brillants mathématiciens n'ayant jamais existé, outre Einstein et Ramanujan, qui a listé les 23 problèmes mathématiques à résoudre pour XXième siècle, bien qu'ils relèvent tous de la logique classique).
En 1960 cette théorie de la démonstration a connu un regain d'intérêt lors de la découverte (fondatrice de l'ère moderne) de la correspondance de Curry-Howard, définissant comme "processus de calcul" la procédure qui consiste à éliminer les coupures définies par Gentzen (pour couper les infinis), faisant des programmes informatiques des démonstrations formelles de la résolution du choix du type des ensembles. Cela a ouvert la voie à l' informatique théorique et donné naissance à de nouveaux modèles (pour de nouvelles logiques). Il résulte principalement de la correspondance de Curry-Howard qu'une partie de la théorie de la démonstration se confond désormais avec la sémantique, ce qui ouvre de nouvelles voies de recherches, et constitue le plus grand tournant jamais prit dans la recherche des fondements de la logique.
La logique linéaire (LL)
Jean-Yves Girard, inspiré par le système T qui est un langage de programmation de démonstration logique développé par Gödel (sans ordinateur, de tête !), innove lui aussi un autre langage de programmation nommé le système F qui permet de résoudre des problèmes plus complexes du lambda-calcul typé du second ordre, conjecturés par Takeuti, le maître qu'il voulait dépasser. Il introduit l'ensemble de nombres 𝔽 ("quelque part entre les entiers naturels (ℕ) et réels (ℝ)").
En 1986, il introduit le modèle de la logique linéaire (LL), qui se base sur une logique sous-structurelle qui décompose et analyse la LC ou la LI de façon calculatoire en un système de types pour le lambda-calcul. Cela permet d'aborder les aspects les plus élémentaires du raisonnement, et offre un cadre unifié pour la LC et de la LI.
La démonstration constructive respecte les contraintes de la LC et de la LI en ne faisant pas appel à l'infini ni au tiers-exclu. Ainsi, démontrer l'inexistence d'un objet ne permet pas de démontrer son existence. Elle est donc associée à un algorithme, en vertu de la correspondance preuve-programme Curry-Howard, qu'on aime bien parce qu'il a dit "prouver, c'est programmer" ☺.
La logique linéaire (ou "logique réelle" selon son auteur) n'est qu'une des applications de cette logique sous-structurelle, et elle se caractérise par le rejet de la règle de contraction (interdiction d'invoquer une même hypothèse plusieurs fois) et de la règle d'affaiblissement (élimination des hypothèses inusitées). Chaque règle est utilisée une seule et unique fois pendant le calcul (tout appel à une fonction ne renvoie qu'un résultat unique). Elle est "consommée" par le calcul, d'où l'opérateur "⊸". Il ne cessera d'ailleurs d'ajouter de nouveaux opérateurs, jusqu'à récemment.
Formalisme
A → B = !A ⊸ BLe membre de gauche est l'espace des fonctions, et celui de droite celui des fonctions linéaire. Se lit : "Toute fonction A dans B est une fonction linéaire de !A dans B", où !A est un espace cohérent associé à A, qui permet de rallier des nombres A qui existent dans la logique classique, via ce qu'il nomme une exponentiation.
Les connecteurs (opérateurs) sont :
- la négation linéaire A⊥
- la conjonction &
- la conjonction multiplicative ⨂ [se lit "ET"]
- la disjonction ⅋ (se lit "OU")
- la disjonction multiplicative 𝓅 [se lit "par"]
- la disjonction additive ⨁ ("OU" qui revient à une association de deux trucs différents)
- le produit semi-direct ⋉ (on peut ajouter ou multiplier seulement des propriétés)
- la flèche linéaire, définie au moyen de la négation linéaire (∼) et de la disjonction multiplicative, ex : A ⊸ B = A⊥ 𝓅 B (source wikipedia...).
- フ (fu) et ヲ (wo) : objectif et subjectif
Il introduit dès lors toute une panoplie d'outillages qui vont avoir une forte résonance pour la logique tétravalente, tels que le principe de réseau de preuves, qui marche aussi bien pour la LC que la LI, et consiste en une déduction naturelle formée par un hypergraphe qu'il faut parcourir. Cela permet d'obtenir une visualisation géométrique des syntaxes formelles.
Réseau de preuves
- le lien Axiome n'a aucun prémisse, et deux conclusions : A et A⊥.
- le lien Coupure a deux prémisses : A et A⊥, et une conclusion.
- le lien Fois a deux prémisses : A et B, et une conclusion : A ⨂ B.
- Le lien Par a deux prémisses, A et B, et une conclusion : A 𝓅 B.
L'hypergraphe est un graphe dont les liens sont orientés, de ses prémisses vers ses conclusions :
- tout énoncé est le prémisse d'au plus 1 lien
- tout énoncé est la conclusion d'au plus un lien.
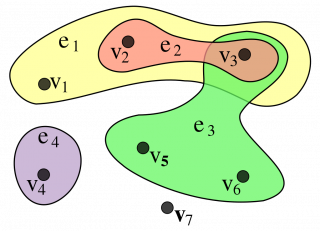
- Hypothèse du réseau : Un énoncé n'est la conclusion d'aucun lien.
- Conclusion du réseau : Un énoncé n'est prémisse d'aucun lien.
A1, A2,... An + B1, B2,... Bn est prouvable, ssi* ∃ réseau connecté où A = hypothèse et B = conclusion.
(*) ssi : si et seulement si
L'algorithme de parcours étudie la connexité entre l'existence de points d'articulation, et permet de choisir le point suivant à visiter, ou passer les sommets déjà visités (les sommets sont les nœuds). Les arrêtes forment une arborescence, et la complexité du parcours de l'arbre est de l'ordre O(n+m) [d'ordre linéaire, pas très élevé], où n sont les sommets et m les arcs entre ces sommets. C'est notamment cela qui est utilisé quand on cherche le trajet le plus court entre différents lieux de livraison de pizzas...
Pont vers la sémantique
Grâce à ce pont jeté entre la théorie de la démonstration et l'informatique théorique, cela a ravivé des outils tels que la réalisabilité, les démonstrations automatiques, et aussi la sémantique.
Explications
La LL nous semble la plus porteuse de sens, donc on s'y attarde un moment ici.
Il faut comprendre que le rejet de la règle de contraction est responsable du fait que le graphe nodal soit orienté. Quand il ne l'est pas, les déductions peuvent se faire dans les deux sens. Or il s'agit d'aller des prémisses vers la conclusion, ainsi les prémisses sont "consommés" par le calcul. C'est la raison pour laquelle ils peuvent servir plusieurs fois, alors qu'en logique formelle, les mêmes prémisses donnant les mêmes résultats, refaire le calcul est inutile.
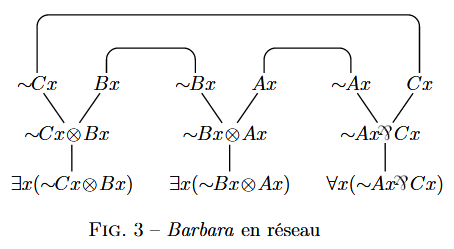
Girard illustre le fonctionnement du graphe nodal avec un exemple minimal, qui est le syllogisme, selon lequel tout système logique a au moins trois objets, deux prémisses et une conclusion. Il en démontre la transitivité. Pour Łukasiewicz, cette transitivité s'exprime par : A ⊂ B ⊂ C (où "⊂" signifie l'inclusion maximale, dont il reste un seul élément qui appartient à A mais pas à B, dans A). On voit que cette formule est fausse. Au final il parvient à prouver à peu près tous les théorèmes et lois mathématiques au moyen de la logique linéaire.
Girard explique l'avancée effectuée par la logique linéaire par le fait de passer du "potentiel" à "l'actualisation des données". C'est à dire, en amont de la construction logique : "plutôt que d'ériger des lois logiques qui préservent la vérité mathématique, on va plutôt partir de ces lois logiques sans en justifier le fondement. Ce critère de correction est à la base d'une relecture radicale de la logique".
Pour lui, la LC et la LI sont imparfaites car basées sur la pérennité.
Girard et la sémantique
Pour Christophe Starchey, "les considérations syntaxiques ne devraient pas prendre le pas sur les considérations sémantiques", bien qu'elle soient (logiquement) moins faciles à étudier. La sémantique ne disposant pas d'outils formels, cela a pousse peu à peu les scientifiques à s'interroger sur la sémantique, la théorie du langage, et donc, sur des questions qui peuvent être philosophiques. Cette interrogation ira jusqu'à se confronter aux problèmes de la mécanique quantique.
Citons ce passage extrait du volume 4 de "Qu'est-ce que l'univers" de Jean-Yves Girard, dans la section "Les fondements des mathématiques" ( wtls.pdf) :
Comment lisons-nous Gentzen de nos jours ? Son travail, qui porte sur l'étude entre une preuve de P et preuve de ¬P (en cas de contradiction), se traduit informatiquement en l'interaction entre un programme (correspondant à la preuve de P) et son environnement (correspondant à la preuve de ¬P), typiquement entre un argument et une fonction. C'est ce qu'on a appelé le paradigme Curry-Howard, ∽1970.
Ces idées devraient être raffinées au moyen de la logique linéaire, ∽1985, qui introduit une symétrie entre le programme et son environnement. La nouveauté par rapport à la logique ancienne (dite maintenant classique) est qu'il s'agit d'un point de vue procédural (la logique linéaire se réfère à ses propres procédures) et non plus réaliste (la logique classique réfère à une "réalité" externe).
Pour lui, l'axiomatisation réduit les conséquences logiques admises, même si elle peut parfois permettre de dégager des hypothèses utiles en réduisant la variété des résultats. La logique et la nécessité sont intrinsèques, tandis que l'axiomatique est extrinsèque. La définition de l'égalité est contraignante sur le plan de la logique. Une démonstration selon Hilbert est un arbre dont les nœuds ont des règles logiques qui sont réduites au seul modus ponens.
Sa critique de la logique classique n'a cessée de se durcir au fil des années, et a fini par formaliser une version 2.0 de la logique linéaire, cette fois radicalement indépendante de toute préconception, remettant en cause le modus ponens, qui est l'art de "poser" des vérités tombées du ciel (appelée "évidence"). Il remarque que l'énoncé 𝒢 (*), n'est pas (simplement) démontrable en logique linéaire. Un raisonnement peut mener à une conclusion correcte tout en étant erroné (paralogisme). L'axiomatique et la sémantique sont comme "l'armée et l'église par rapport à la démocratie". La quantification du premier ordre opérée par une équivalence linéaire n'est pas une quantification du second ordre déguisée, et n'est pas sujette aux interrogations du deuxième ordre. Pour lui la logique objective est un "délire schizophrène". Il oppose, conformément à ce que sous-tend la théorie de l'incomplétude, le sujet et l'objet, l'intrinsèque et l'extrinsèque, l'essentialisme (= arrogance) et l'existentialisme (= preuve sans preuve), la preuve et l'épreuve, et développe ce qu'il appelle un modèle de réfutation, qu'il nomme le "déréalisme".
(*) 𝒢 est un énoncé du premier théorème d'incomplétude qui est égal à sa propre négation, et donc n'est pas démontrable. Il stipule que la preuve de la consistance d'une théorie implique son inconsistance, ce qui est un sacré paradoxe.
Il faut dire en passant que la plupart des logiciens sont devenus fous.
Le pauvre Gödel est mort d'inanition parce qu'il avait développé et inventé une nouvelle maladie mentale, la peur que la nourriture soit empoisonnée...
Avant de poursuivre, précisons que pour Girard tous les autres modèles logiques sont de la chiotte, en particulier celle qui sert pour l'IA et encore plus la logique modale ou paraconsistante, qui n'est d'un déguisement effarant de la logique classique. C'est pas grave, on va les étudier quand même.
La logique modale (LM)
La logique intuitionniste (LI) peut être construite sur la logique aléthique comme une logique modale. La logique modale est un fragment de la logique de premier ordre, qui étend la logique propositionnelle (l'étude des relations logiques entre les propositions = LC) au moyen de modalités dites aléthiques, qui servent à définir "la vérité". C'est la première fois depuis le début de l'histoire des logiques que nous visitons un autre pays que la France, les États-unis. Il y a là aussi des notions intéressantes à glaner.
Formalisme
La logique aléthique accepte les connecteurs suivants :
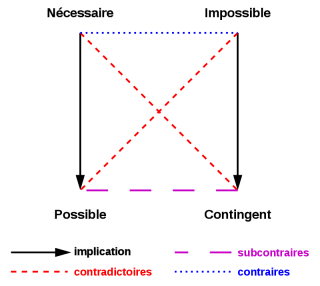
- nécessité : ☐
- contingence : ¬☐
- possibilité : ◊
- impossibilité : ¬◊
Il en résulte que, pour A = "les élèvent travaillent" :
- ¬☐A : "il est non-nécessaire que A"
- ¬◊A : "il n'est pas possible que A"
- ☐¬A : "il est nécessaire que [les élèves (ne) travaillent] pas"
- ◊¬A : "il est possible que [les élèves (ne) travaillent] pas"
- "nécessaire" peut être faux sans être contradictoire.
- "contingent" peut être faux sans contradiction.
Axiomes
La logique possède une variété de champs auxquels sont associés des propriétés :
- épistémique (porté sur les connaissances) : connu, contestable, exclu, plausible, connaissance commune ou partagée...
- déontique (sur les obligations) : obligatoire, interdit, permis, facultatif...
- temporelle (ce qui va être très intéressant) : toujours, un jour, jamais, demain, jusqu'à ce que, passé, hier...
- doxastique (sur les croyances) : cru, croyance commune, évidence...
- contrefactuelle : Si A est vrai alors A n'est pas vrai
- dynamique (effet d'action) : P est vrai après exécution de A.
On le voit, cela s'approche beaucoup des appétences de la logique tétravalente, qui admet la phénoménologie, temporelle ou d'action, et qui rendent le graphe indéterministe.
Les axiomes de la logique modale sont, par ordre de "solidité" : K (la distribution), D (nécessité implique possibilité), T (le fait implique la possibilité), puis S4, S5 et B. Un système modal est "normal" s'il accepte l'axiome K, et la règle de nécessitation RM comme règle d'inférence (wikipedia).
Le mode "temporel" est très intéressant, puisqu'il accepte les propriétés "toujours", "un jour", "jamais", etc. qui ont la particularité de transformer un résultat "vrai" ou "faux" lorsque la condition est appliquée. C'est donc une logique non-monotone (LNM, voir plus loin).
Φ ⋃ Ψ : "la formule Φ est satisfaite jusqu'à ce que la formule Ψ le soit"
Il s'en déclinent la logique temporelle linéaire (LTL) [1977] et la logique temporelle (CTL*) [1981].
LTL est une logique monadique de second ordre avec un successeur (1S1). Une proposition peut être satisfaite sous condition du temps T. Elle est utilisée en model checking, pour valider des actions.
CTL* (Computation-tree logic *star*) est une logique temporelle linéaire où une formule est définie selon la logique des branchements (branching logic). Elle combine librement des quantificateurs sur chemins et des opérateurs temporels. La sémantique repose sur une structure de Kripke, dont l'auteur est responsable de "l'axiome K", et aussi l'initiateur du principe de "mondes divergents" que l'on va voir juste après, avec la trivalence.
La structure de Kripke
La structure de Kripke est un modèle de calcul proche d'un automate fini non déterministe. (C'est là que ça devient intéressant). Elle est utilisée en Model-checking pour représenter le comportement du modèle, et un graphe orienté dont les nœuds représentent les états accessibles du système, et les arcs représentent les transitions entre les états. Les logiques temporelles sont généralement interprétées dans une structure K, qui est constituée d'un quadruplet S, I, R, L, où :
- S = ensemble des états finis
- I ⊆ S = ensemble des états initiaux
- R ⊆ S ⨯ S = relations de transition
- L : S → 2AP = fonction d'étiquetage ou d'interprétation.
Note : Cette dernière notion, l'étiquetage, va aussi énormément nous servir.
La sémantique de Kripke
La logique modale est dès lors très connectée à la sémantique, plus particulièrement "la sémantique de Kripke". Dans sa "la nouvelle théorie de la vérité", il crée une distinction selon laquelle une convention peut être "connue a priori" et contingente, alors que les propositions des sciences peuvent être "a posteriori connues".
Il étudie en particulier les noms propres, qui sont un vieux sujet de la philosophie des sciences. Pour Kripke, un nom propre décrit une même personne dans tous les mondes possibles et imaginables, tandis que les descriptions ne servent qu'à le définir. Ce qui importe pour lui n'est pas ce que nous savons, mais le nom qu'on lui donne. Par exemple Jésus peut avoir ou ne pas avoir des faits d'armes à son actif, cela ne change rien à sa vraie nature, même si nous en ignorons un grand nombre d'aspects.
Dans sa théorie de la vérité, un langage peut contenir le prédicat de "vérité", ce qui est impossible dans la sémantique de Tarski (qu'on va voir ensuite). Il définit comme "vérité" l'union de toutes les étapes de la description. Après une infinité d'étapes, le langage atteint un point fixe, qui peut être considéré comme son propre prédicat de vérité. Ce prédicat demeure non-défini pour les énoncés qui ne peuvent pas se simplifier, tels que "la neige est blanche", qui est une vérité, et cette vérité est vraie.
Note personnelle : La théorie de Tarski ne brise pas, mais révèle les frontières entre le connu et la vérité, tandis que celle de Kripke définit le terme de vérité relativement à l'ensemble à dans lequel elle est considérée, ce qui ravit les théoriciens classiques. Il aurait dû dire "théorie de la vérité relative" mais ça n'aurait pas été aussi vendeur ! Le problème qui nous apparaît clairement est d'ordre topologique, et on pourra, dans une prochaine partie, distinguer la vérité de la réalité, et la nature des réalités potentielles.
La (les) logique(s) polyvalente(s) (LP)
La logique multivalente est basée sur les calculs propositionnels (l'étude des relations logiques entre les propositions et de leur formule d'assemblage) et le calcul des prédicats, qui remonte à Frege (au tout début) :
ᗄx gentil(x) et ∃x∀y amis(x,y)« Tout x est gentil » et « Il existe un x tel que pour tout y, x est ami avec y »
Elle a été créée pour répondre aux problèmes de la physique quantique, en prévoyant l'usage des qubits, bien que dans sa formulation actuelle elle ne soit pas encore exploitée à cet égard. Elle est étudiée dans le contexte du rejet du tiers-exclu et des contradictions.
Apparentées à la logique modale, les logiques polyvalentes sont principalement étudiées dans le contexte de la mise en question générale des principes du tiers exclu et de contradiction.
Sa syntaxe utilise des identificateurs (termes symboliques) et des relations (prédicats et formules), et sa sémantique est faite d'énoncés qui expriment des relations entre les éléments (des modèles).
La principale caractéristique des logiques polyvalentes "à nombre infini de valeurs" est qu'elles sont complètes (au sens de la complétude de Gödel) et leur satisfaisabilité est décidable (c'est à dire qu'elles sont cohérentes).
La trivalence
Un exemple de trivalence permet de mettre en évidence son approche épistémique, en faisant appel à la notion de "vrai ou faux". Par exemple, l'état du chat de Schrödinger est assemblé dans un nouvel état "mort|vivant", qui constitue "un monde", auquel le monde dans lequel "le chat est vivant" peut accéder.
Les logiques partielles
La trivalence n'est qu'une des déclinaisons de la logique multivalente, il y en a d'autres, telles que la logique partielle (LP1), qui interprète la troisième valeur comme "ni vrai ni faux", et la logique paraconsistante (LP2), qui interprète la troisième valeur comme "vrai et faux".
La logique partielle (LP1) est fondée sur la logique de Hoare, créée en 1969, qui est une méthode formelle (logique de raisonnement fondé sur l'informatique) dotée d'un formalisme qui permet d'automatiser les preuves des programmes et notamment leur correction (il faut comprendre que parfois le programme ne se termine pas, d'où le "ni vrai ni faux"). Son axiomatique est le triplet de Hoare : Précondition, instruction, post-condition.
La section suivante expliquera en quoi les logiques polyvalentes sont "partielles" en terme général.
La logique paraconsistante (LP2) admet que "d'une contradiction se déduit n'importe quoi". Cette logique est utilisée pour étudier les contradictions en sémantique, épistémologie ou même en génie logiciel (d'où le "vrai et faux").
Développons cela, car il y a des choses intéressantes à glaner.
La logique paraconsistante (LP2)
Cette section va engendrer plusieurs itérations...
Le terme de " paraconsistant" signifiait "quasi" dans l'esprit de son inventeur en 1976, Miró Quesada, mais est finalement devenu "au-delà". Le terme "consistant" signifie en anglais "cohérent".
La LP2 est un système logique (formules + règles) qui tolère les contradictions. Son champ d'application est ceux de la sémantique, l'épistémologie, la gestion des connaissances d'une IA, la logique déontique et méta-éthique, et le génie logiciel.
Cohérence
La cohérence logique d'une théorie axiomatique peut se définir :
- soit par l'inférence de la déduction
- soit par référence à la sémantique de la théorie.
La première définition est syntaxique. Ses déductions sont des objets finis, sa consistance repose sur le fait de ne pas forcément reposer sur tous les énoncés de son langage. La seconde définition utilise la théorie des modèles (une structure mathématique dons laquelle son langage s'interprète), et qui satisfait tous les axiomes de la théorie. Ces deux définitions sont rendues équivalentes par le théorème de la correction, et la théorie de la complétude (Wikipedia).
Contradictore sequitur quodlibet
"D'une contradiction se déduit n'importe quoi". Ce fondement de la logique paracohérente repose sur le principe de l'explosion, que nous allons expliciter.
Dans la proposition "tous les citrons sont jaunes" + "certains citrons ne sont pas jaunes", les deux segments sont considérés comme "vrais". On peut poser une alternative "les citrons sont jaunes OU le père noël existe". La déduction renverra dont la réponse : "Le père noël existe", si la contradiction est relevée.
Le principe de l'explosion
Le principe de l'explosion est ce schéma de raisonnement (que nous venons de montrer) qui montre les limitations des règles d'inférence classiques. Il consiste à poser deux prédicats contradictoires, et d'en contrebalancer un par une proposition tierce. Dans ce contexte, la résolution des paradoxes peut conduire à une explosion combinatoire, comme l'illustre l'exemple suivant :
Deux conducteurs qui arrivent à un carrefour. A s'avance car il connaît le code de la route et sait qu'il a le droit ; B s'arrête car il voit A et connaît le code de la route ; de plus il sait que A connaît le code de la route et sait qu'il a le droit. Et B s'avance car il sait que A sait qu'il connaît le code de la route et qu'il a le droit, et sait que B sait que A sait que B sait que A... etc.
Donc, la résolution d'une contradiction peut engendrer deux réponses : soit une réponse absurde, soit une réponse infinie, "une explosion". "Ex Falso quodlibet" est une règle de la LI (logique intuitionniste) et d'autres logiques non-classiques. Certaines d'entre elles tentent de gérer ces cas particuliers comme la logique non-monotone ou la logique minimale.
(La suite logique de ceci se trouve à la section "Formalisme de la LP2", mais d'abord, glanons quelques notions complémentaires).
La logique minimale (LMIN)
Il s'agit d'une LC démise du tiers-exclu et à la fois du principe d'explosion. Elle se distingue de la LC et de la LI par son traitement de la négation et des contradictions dans le calcul des propositions (des prédicats). En LMIN, simplement, il n'y a pas de négation possible, et le rejet de la contradiction rend possible le raisonnement par l'absurde. (Note : beaucoup de gens utilisent sans le savoir la LMIN). (Ses modalités sont aussi celles de la logique paraconsistante qu'on va développer ensuite, dans la section qui parle de Tarski).
La logique non monotone (LNM)
La plupart des logiques formelles (LC, LI, LL), sont dites "monotones" car l'ajout d'un fait ou d'un axiome n'interfère pas avec les résultats déjà obtenus. Les logiques doxastiques ne permettent pas de réviser les connaissances, contrairement aux logiques épistémiques, à laquelle appartient la LNM.
Exemple de révision des connaissance, avec cet énoncé : "Si X est un oiseau, mais pas si X est un manchot, alors X vole" + "Titi est un oiseau". Le résultat sera "Titi vole". Si on ajoute "Titi est un manchot", on peut diminuer la base des faits déduits, et les remettre en cause.
Note de geek : C'est à cause de cet écueil qu'a été élaborée la clause qui force la fermeture à l'accès aux bases de données durant l'exécution d'un programme.
La logique épistémique (LE)
C'est une logique modale (LM) qui permet de raisonner sur les connaissances. Elle utilise la "modalité K", accepte toute proposition de la LC et de la LI, et est complétée par la logique des connaissances communes, selon laquelle la connaissance peut être "partagée par un groupe d'agents dont tous savent qu'ils la partagent".
L'idée de Kripke est d'introduire la notion de "mondes possibles", qui peuvent s'apparenter à des super-ensembles théoriques. Dans chaque monde, la réalisabilité indique quelles propositions sont vraies ou fausses. Un agent peut imaginer d'autres mondes possibles (on retrouvera cette notion de mondes et d'univers dans la logique homotopique).
Note : C'est l'apparition des logiques épistémiques qui a donné lieu au néologisme "épistémologie".
Le modèle K :
- un univers 𝒰 dont les éléments sont notés ℳ (des mondes, associés à un modèle M)
- un agent, affecté à chaque relations
- une relation de réalisabilité (symbole ⊩) entre ℳ et 𝓅 (une proposition)
M ⊩ 𝓅
une proposition 𝓅 est valide pour tout modèle M et tout monde ℳ de ce modèle.
Axiomes :
- K : l'agent peut faire des déductions
- T : les agents connaissent des choses vraies
- 4 : si A sait quelque chose, alors il le sait
- 5 : si A ne sait pas quelque chose, alors il sait qu'il ne le sait pas
Note : l'axiome 5 rappelle Socrate. Il semble important pour nous.
La conjonction infinie des connaissances (c'est à dire l'explosion donnée par un paradoxe, dans l'exemple des automobilistes à une intersection) est une extension de la LE.
Formalisme de la LP2
L'incohérence du principe de l'explosion, qui en logique formelle construit trivialement un théorème, n'est pas permise en LP (logique paracohérente). Le calcul des propositions est donc considéré comme "plus faible" qu'en LC.
Note : ici nous répétons ce que dit Wikipédia, mais il serait plus logique de dire que "l'incohérence du principe de l'explosion est permise en LP, ce qui la rend plus faible que la LC", à moins que le terme "incohérence" ne signifie "le rejet". Il y a aussi quelques fautes d'orthographes et des mots en double dans ces données...
Les propositions se doivent d'être prudentes dans leurs inférences (voir LMN). Elles doivent utiliser un méta-langage, comme celui de Tarski, qui interdit l'autoréférence, qui est à l'origine des paradoxes.
Exemple d'autoréférences : "Cette phrase est un mensonge", "la permanence de impermanence".
Note : Le premier exemple est celui qui a inspiré Gödel pour ses théorèmes d'incomplétude). La forme mathématique de l'autoréférence, l'imprédicativité, anima également les conversations entre Henri Poincaré et Bertrand Russell.
De même, les déclarations qui proviennent d'expériences ne sont pas de la logique : "il n'y a pas d'absolu dans l'absolu". Ici on voit que le même terme va revêtir deux acceptions légèrement distinctes.
Tarski et la théorie de la vérité
(itération impromptue)Le théorie de la vérité a jeté les bases de la sémantique et de la théorie des modèles, au début du siècle dernier, ainsi qu'à l'épistémologie [ludique] de Karl Popper.
Il montre que la notion de vérité des langages formalisés ne peut être définie dans ce même langage, ce que l'incomplétude de Gödel a prouvé mathématiquement (toujours en considérant la logique formelle comme vraie). "Ce chien est noir" n'est vrai que si c'est réellement le cas. Une vérité doit nécessairement être établie dans un métalangage plus riche que celui où elle est démontrée.
Note en passant, juste pour dire : les conversations informelles ne construisent leur vérité que sur des sous-entendus implicites qui sont passablement inaudibles pour personnes qui ne sont pas familiarisées à cet exercice, par exemple, avec le métalangage qui révèle la violence symbolique. Ici, au lieu de "méta-langage" on ferait mieux de parler d'immersion dans une culture.
La conception sémantique de la vérité de Tarski joue un rôle important dans les logiques modernes et dans beaucoup de philosophies contemporaines du langage, de même qu'il est aussi passablement réfuté.
Le dialethéisme
Les paradoxes, comme celui de Russell, conduisent à des explosions. Car, si une contradiction est vraie, alors toute proposition est vraie. En LC on interdit arbitrairement les propositions contradictoires, en révisant les axiomes. Le dialethéisme permet, lui, d'utiliser le schéma de compréhension non restreint, affirmant que tous les objets ayant une même propriété forment un ensemble, et donc, en acceptant les contradictions comme vraies.
Différence entre logique paraconsistante et dialethéisme :
Source Graham Priest : "La paraconsistance est une propriété d'une relation de conséquence alors que le dialethéisme est un point de vue sur la vérité. Le fait que l'on puisse définir une relation de conséquence non-explosive ne signifie pas que certaines phrases sont vraies. Le fait que l'on puisse construire un modèle où une contradiction est vraie mais où toutes les phrases du langage ne le sont pas (où c'est le cas dans un certain monde) ne signifie pas que la contradiction est vraie en soi. Par conséquent, la paraconsistance doit être distinguée du dialethéisme."
Formalisme de la LP2
(revenons-en à nos moutons)Ainsi, la contradiction, et plus particulièrement la valeur "vrai et faux" engendre une "explosion". Cette explosion est due à la cohérence entre eux des axiomes suivants (avec "⊢" qui signifie "prouve", "démontre") :
- introduction de la disjonction : A ⊢ B ⋁ B
- syllogisme disjonctif : A ⋁ B, ¬A ⊢ B
- transitivité de la déduction, ou "règle de coupure" : ⎾ ⊢ A; A ⊢ B ⟹ ⎾ ⊢ B
1) Le paralogicien rejette le principe de syllogisme disjonctif. De même, le dialéthéiste dit : "Si ¬A est vrai, alors A ne peut l'être". Donc, A ⋁ B ne peut être vrai que si B l'est également. Cependant, A et ¬A peuvent être vrais.
2) Si on coupe l'introduction de la disjonction, cela interdit le raisonnement par l'absurde, mais le tiers-exclu est conservé, de même que l'idempotence (une mauvaise et une bonne chose).
3) Une autre approche consiste à rejeter les deux, comme en LL (logique linéaire), et donc en utilisant des connecteurs dédiés.
Ces trois principes pris ensemble ont pour conséquence le principe de l'explosion. Donc l'un d'eux doit être [semble devoir être] abandonné :
- Reductio ad absurdum : A → (B ⋀ ¬B) ⊢ ¬A
- Règle d'affaiblissement : A ⊢ B → A
- Élimination de la double-négation : ¬¬A ⊢ A
L'élimination des deux premières ont été envisagées, sans grand succès, quant à la troisième, elle est (évidemment) très discutée.
Mathématiques amusantes : lien vers une démonstration par l'absurde que Pythagore est faux concernant la diagonale du carré √2 : deleze.name. La démonstration par l'absurde marche très bien en LC, mais elle sera à rejeter en logique tétravalente.
La logique floue (LF)
Enfin, la logique floue est une logique polyvalente "de basse intensité" (peut-on dire) qui s'oppose aux logiques modales. Fondée en 1965 par Lofti Zadeh, c'est un outil écrit pour l'intelligence artificielle, mais qui sert le plus souvent pour l'ABS des voitures, la robotique, la circulation routière, la météorologie, le contrôle aérien, la prévention des risques, etc., bref partout où la loi décide de limites arbitraires.
C'est une extension de la théorie des ensembles classiques aux ensembles définis de façon imprécise. La LF bâtit un modèle complet de propriétés et de définitions formelles, qui peut se réduire à des ensembles de la LC quand les valeurs deviennent binaires. C'est donc une logique "solide", plus facile à implémenter que la logique probabiliste (LProb), et qui remplace la valeur de vérité par un degré de vérité, échelonné de 0 à 1. Par exemple pour savoir si "la vitesse est élevée", on décide arbitrairement des limites dont la valeur "légale" est une médiane, et le calcul renvoie 0% en-dessous de 70Km/h, 50% à 80Km/h et 100% à 90Km/h.
Un mot sur la sémantique
La sémantique n'est pas à proprement parler "une logique", cependant grâce à l'informatique, cet adjoint aux logiques s'enrichit énormément d'outils capables de relier concrètement les mots en fonction du signifié. Un graphe ontologique permet facilement de parcourir d'énormes quantités de données pour y adjoindre des résultats qui sont similaires, comme le font les moteurs de recherche.
Ce sont aussi des connaissances, avec la science du langage, dont chacun devra avoir conscience pour se figurer les schémas qui s'érigent dans la tête d'une IA quand on lui adresse un énoncé... [🤖 Ceci est une locution prépositionnelle de condition].
La théorie des types homotopiques (HTT)
Il semble quand même important de ne pas terminer cet exposé sans évoquer la dernière émanation pondue par nos brillants cerveaux qui, aujourd'hui encore, cherchent à fonder les mathématiques sur des bases logiques. De ce fait les ouvrages portent toujours le même nom, "fondement des mathématiques", et ici cette histoire est encore très récente.
La théorie des types homotopiques est une sous-jacence de la logique intuitionniste. Si en LC on utilise des objets qui peuvent être des ensembles, en LI il s'agit de construire un résultat à partir de briques élémentaires et de règles. Chaque combinaison de règle de construction donne lieu à une fonction, qui correspond exactement à une fonction informatique (un algorithme). Donc, l'axiomatique de Peano de la LC disant que S0=1 (successeur de zéro) devient une fonction add(n,0) ≡ n. L'usage de "≡" signifie que c'est une égalité définitionnelle, là où "=" est une (bête) égalité propositionnelle.
Un type est une structure informatique qui suppose un constructeur et une induction. Il existe donc des outils spécifiques pour passer d'un type à un autre. Les types les plus évidents sont par exemple les nombres et les lettres. En informatique, si on demande :
$a='texte'; $b=$a[2]; //$b='x'; Il comprend tout seul qu'on demande le deuxième successeur de la zéroième lettre du texte. ("//" est un commentaire de code, c'est ce que le code sait déjà).
Pour en comprendre vaguement le fondement (n'ayant pas lu l'ouvrage de référence Homotopy Type Theory), il faut repartir des nombres relatifs.
Admettons un point de départ (0) auquel on ajoute 1 puis on retire 1, le curseur revient au point de départ. On note 𝒶 = 𝒶 le chemin pour aller de 𝒶 à 𝒶, où le signe "=" devient une preuve du cheminement. Ce résultat peut être la concaténation du cheminement de 𝒶=𝒷, de 𝒷=𝒸, et de 𝒷=𝒶. L'intérêt est qu'on peut parcourir la boucle dans les deux sens (dit comme cela, évidemment ça ne paraît pas surprenant), ce qui permet au final de définir "le cercle" comme l'association d'un point et d'une boucle, et donc de deux preuves du cercle. C'est intéressant parce que le cercle est défini sans forme pré-établie.
De fait, cette théorie des types (qui relègue l'ancienne à la préhistoire) permet de structurer convenablement la théorie du lambda-calcul de Church (1936). Ainsi on a une hiérarchie entre, de bas en haut, les procédures, les objets (qui sont des assembleurs), et la théorie des types structurés. Finalement un "type" est une généralisation des catégories, telle que postulée par la théorie des ensembles.
Dans la théorie des types, les connecteurs (→, +, x) sont associés à des constructeurs et des principes d'induction. Du coup, tout théorème sera un type, et prouver un théorème revient à construire un élément de ce type. La négation de ceci est que si on associe un type Zéro, inhabité, à un autre type X, alors c'est absurde car X est forcément habité : ¬X ≡ X → 0 (donc pas associable).
Mine de rien la théorie des types permet de gérer le tiers-exclu comme une propriété, comme ici dans cette double-négation :
Π X ∈ 𝒰 ((X → 0) → 0) → XSi on suppose qu'il existe un élément de ce type dans l'univers 𝒰, alors cela revient à accepter le tiers-exclu, et donc supposer l'axiome du choix.
Dans ce cadre, le "∃" (il existe) platonicien de la LC devient un élément prouvable. Mais si on tient absolument à revenir à l'arithmétique classique, on peut le faire par la troncature ||X||, comme dans la LL. Mais dans ce cas, si X → ||X|| (X prouve la valeur de X), il est faut de dire que ||X|| prouve X. (Ce que tout le monde devrait savoir !!)
Bref, c'est un développement en pleine effervescence, et ils n'ont pas fini de rigoler...
Sur la théorie des types homotopiques, vous aurez les idées plus claires avec cette vidéo : youtube
La logique quantique
L'expression "Dieu ne joue pas aux dés" de Einstein, résultait de l'observation du comportement des particules subatomiques, comme l'électron ou le photon, qui étaient une onde avant qu'on ne les observe, et qui devenaient une particule sitôt qu'on les mesurait. À ce moment-là, non seulement l'onde disparaît subitement, toutes les trajectoires probabilistes sont effacées de la réalité, et la seule chose qu'on est autorisés à observer est une bête particule tout à fait innocente.
Le plus étrange est que la propriété de cette particule découle entièrement du hasard, cependant, toutes les fois où on mesurera cette même particule, elle se rappellera du mensonge qu'elle vous a fait et sortira toujours la même et unique propriété. C'est pour le moins déconcertant.
Alors les scientifiques, qui aiment pousser l'expérience jusqu'au bout de ce qui est possible pour être certains qu'ils ne sont pas les objets d'une ruse, et qui cherchent à découvrir cette ruse, ont élaboré une méthode pour mesurer l'état d'un photon ayant traversé un stupide filtre polarisant, qui filtre les photons en fonction de leur spin. Selon la théorie, le filtre polarisant empêche cinquante pourcent des photons de passer, et il faut déterminer quelles sont ces "variables cachées".
Si vous connaissez les filtres polarisants vous savez qu'il suffit de les faire pivoter pour régler la quantité de photons filtrés, de 50% à 100%, et que les reflet du soleil sur l'eau sont déjà polarisés, et donc mieux filtrés. Ou que les lunettes de soleil de mauvaise qualité on des polarisations variables qui permettent de voir ou cacher l'écran du téléphone.
Pour faire cette expérience ils placent deux filtres à équidistance de la source lumineuse, qui en soit est déjà un prodige de technologie, et mesurent l'état du photon après être passé par chacun de ces filtres. En théorie, d'une paire de photons envoyés, il y a quatre possibilité, soit le deux passent, soit les deux ne passent pas, soit un des deux passe.
La déduction de l'expérience est simple à faire, si la théorie quantique est correcte, et si le principe de "localité" est respecté (selon lequel il n'y a pas d'action à distance opérée sur le photon par la pensée, qui agirait plus vite que la vitesse de la lumière), alors il existe des variables cachées.
De fil en aiguille, il a fallu attendre une publication de 1965 pour donner l'idée de cette expérience, et attendre jusqu'à 2015 pour qu'elle en déclare officiellement le résultat, selon lequel, le problème, il est dans la tête des gens, et non dans la mécanique quantique. C'est à dire que s'il existe des "variables cachées", alors elles sont locales, du moins tel que les résultats sont interprétés.
En effet l'expérience montrait que les photons avaient toujours rigoureusement le même comportement quel que soit l'endroit où on faisait l'expérience, et ce, même si on inclinait le filtre polarisant "plus vite que la vitesse de la lumière" en cours balade du photon dans l'espace. De là, a été admit, et amplement popularisée, l'idée selon laquelle les photons étaient "intriqués", c'est à dire qu'ils agissaient comme un seul arnaqueur.
Mine de rien, cela dit en passant, cette recherche théorique servant uniquement au bonheur des scientifiques, une fois de plus, a trouvé des applications pratiques bien plus vastes et prolifiques que celles qui sont commandées objectivement. Ceci n'est pas une remarque à prendre à la légère, car tout est lié (on le verra dans l'article suivant).
En tous cas, les scientifiques viennent de mettre le doigt sur "quelque chose" de véritablement transcendant. Il existe des actions sans contact. Cela suppose toute une refondation de notre conception de la réalité, rien que ça ! En pratique, la question est "les objets sont-ils vraiment là, sous nos yeux, tels que nous les percevons ?", en d'autres termes : "existe-t-il une réalité extérieure à nous, dont nous sommes que de passifs observateurs ?".
Sur l'expérience de Alain Aspect : scienceetonnante.com
Conclusion sur l'histoire de la logique
On peut s'en étonner, ou pas, mais l'avancée des logiques se produit à petits pas, "de proche en proche" (citation anticipée), toujours sur des bases mathématiques et formelles, bien que précisément ces bases soient sans cesse reformulées, en ensembles, en groupes, en catégories, en objets, en fonctions, en mondes ou en types...
Tous les éléments constitutifs de la logique tétravalente telle qu'elle nous a été présentée sont présents dans l'histoire. En fin de compte cette présentation n'est qu'une information de type structurelle, c'est à dire un assemblage nouveau de principes connus. Le reste est encore à découvrir.
On a pu voir que la fabrication d'une logique repose sur un modèle, cohérent et complet, qui est proto-mathématique, et d'axiomes (qui peuvent être globaux ou pontcuels). Par chance, les modèles se déduisent automatiquement des programmes, et les axiomes sont totalement libres.
Il est difficile de positionner la logique tétravalente dans cet arborescence de solutions, puisque chacune d'elles possède une bribe de fondation aux questions qu'elle peut résoudre. On ne pouvait pas, toutefois, envisager de se lancer dans la construction d'une logique tétravalente sans glaner ici ou là les formalismes et les nombreux termes obtenus de toutes ces études.
Note de Norman : En fait, si! À mes yeux, il eût mieux valu ne pas explorer/exposer les multiples branches de l'arbre des logiques inventées par nous, et se contenter d'exposer la logique tétravalente comme nos visiteurs me semblent l'avoir fait, c'est-à-dire sur la base d'une théorie "intuitive" (= facile à comprendre) des ensembles ayant peu d'axiomes et peu de règles. L'histoire des logiques inventées par les terriens sert plus à semer la confusion [à cause du foisonnement de termes et de la complexité inutile du vocabulaire correspondant] qu'à exposer ce qui est nécessaire, c-à-d: le mode d'emploi de la logique tétra de nos visiteurs.)
Pour l'instant, ils semble que la meilleure inspiration pour la logique tétravalente sera la logique linéaire, dont l'argumentation repose sur le rejet de l'ensemble des logiques présentées ici.
Note de Norman : (peut-être... Je n'en suis pas persuadé... Je préfère m'en tenir aux ensembles...)
Comme à chaque fois, comme pour toujours, à moins qu'une étude n'ait pour effet de mettre un terme à une recherche qui s'avère finalement impossible (ce que Gödel a fait en mettant fin à la résolution des paradoxes stupides), les avancées scientifiques, quel que soit leur succès, ont pour principale utilité de fournir de nouveaux outils aux évolutions suivantes.
Les pistes qui nous restent à explorer sont celles, philosophiques, de "la vérité", de la linguistique, et de nouveaux discernements qui restent à faire pour certifier le caractère particulier de la logique tétravalente. Il nous paraît évident qu'elle répond de façon favorable aux problèmes restés en suspens, qui font de chaque logique un particularisme adapté à des cas de figures de plus en plus étroits, bien qu'attachés à des secteurs de plus en plus décisifs tels que l'intelligence artificielle.
Il faut pouvoir se départir de ces limitations et contradictions pour proposer une solution qui unifie la cascade qui tend vers l'infini de solutions particulières au problème général de "la logique".
La philosophie des sciences
On le voit, les chemins pris par la conception de la logique vont en s'étoffant de multitudes d'instances (un terme du second degré) de toujours le même principe, multiplicateur, qui permet d'aller toujours plus "bas" dans la résolution d'un calcul. C'est d'un vif intérêt quand il s'agit de se départir de contradictions logiques qui consistent à résoudre le problème pour savoir s'il peut être résolu...
Whitehead
Pour finir ce tour d'horizon des écoles de la logique, revenons sur Ernest Whitehead, le professeur de philosophie du jeune Bertrand Russell, qui ne se voyait pas écrire de grands ouvrages, mais qui finalement a ouvert la voie à une école de la philosophie scientifique. Il a d'abord introduit la notion d'"abstraction extensive", considérée comme fondamentale pour la branche de l'informatique et de l'ontologie, qui consiste à établir des relations entre les ensembles.
Son point de vue est qu'on ne pouvait dissocier la science et la philosophie comme c'était toujours le cas. En ce sens il a préfiguré ce que Teilhard de Chardin a fini par avouer qu'il admettait comme vrai à la fin de sa carrière, quand il n'avait plus peur des moqueries, en évoquant une grande unité. Whitehead a tissé le lien entre épistémologie et métaphysique en rejetant "l'identification de la nature aux outils mathématiques utilisés pour caractériser leur structure relationnelle". Cette notion est abordée d'une manière ou d'une autre par Girard, Kripke, Gödel, Tarski...
Selon lui tout objet est une "signification idéalisée de ce qui est stable". Il définit le point géométrique comme "une haute abstraction qui ne correspond pas à la réalité dont on peut faire l'expérience" (Ce qui rappelle le rejet du point géométrique abordé dans la D59-1). Pour lui les réalités fondamentales de la nature ne sont pas des objets mais les événements, c'est à dire à la fois les objets et la raison de leurs interactions. Il lui paraît superflu de vouloir étudier l'un sans l'autre (et il a bien raison).
Il introduit le principe de préhension, c'est à dire de "perception sans cognition", qui s'oppose à ce qu'il nomme (et est fier de nommer) "le matérialisme scientifique dogmatique". Pour cette raison, le progrès social ne peut (pas du tout) relever des sciences sociales.
Il fait remarquer que les scientifiques font constamment des suppositions métaphysiques sans le savoir, mais que ces hypothèses ne sont pas facilement visibles étant donné qu'elles ne sont ni formulées correctement, ni remises en cause ou questionnées, ni encore moins contestées (ce qui n'a plus été vrai dans le cas de la découverte de l'intrication).
Pour lui, "les chercheurs doivent sans cesse ré-imaginer leurs hypothèses de base sur la façon dont fonctionne l'univers, pour que la philosophie et la science puissent faire de réels progrès". "Seule l'expérience rompt le matérialisme cartésien entre l'esprit et la matière". Il estime que la philosophie ne devait pas être divisée en spécialités telles que la physique, l'éthique ou l'algèbre... et nous voyons cent ans plus tard comme les variétés de logiques tendent à devoir s'intéresser à la sémantique, et à la notion de "vérité".
Tout comme Gödel, qui se demandait, angoissé, s'il était en droit d'outrepasser les limitations voulues par Dieu pour comprendre l'univers, Whitehead s'intéresse à la théologie en définissant Dieu comme à la fois immanent et transcendant, c'est à dire qui agit à la fois sur les causes et sur les finalités. Il semble bien qu'à un moment ou à un autre, Dieu va devenir une partie utile de la logique. Et si le début et la fin étaient intriqués ?
Il définit la pensée comme la méthode qui consiste à tester des hypothèses de proche en proche, et le langage comme l'opération qui participe à une "élévation méthodique salutaire". Le temps, enfin, n'advient que lorsqu'il se produit un événement, et relève donc de la psychologie. Sur ce point, il a été un visionnaire, mais cela n'est pas encore officiel.
Raymond Ruyer
Un autre philosophe, au milieu du siècle, Raymond Ruyer, tout aussi humble et encore plus oublié, fait un peu les mêmes remarques, en allant un peu plus loin dans la formalisation du concepte de ce qui agit "de proche en proche", nommé aussi "la localité". Il distingue les actions par contact, qui sont l'activation des chaînes de conséquences, de l'action sans contact, qui procède de la structuration des choses, régie par le temps, et par une certaine source d'information, immatérielle.
Note : Aujourd'hui, "l'information" est considérée comme "un état de la matière", et même si c'est capillotracté, cela ouvre une perspective dont Ruyer supposait déjà l'existence. Cela nous conduira à admettre l'existence d'un champ adimensionnel servant de support à l'information, dont notamment les lois physiques et biologiques.
Il prend l'exemple de l'œuf qui germe et note qu'il serait impossible, autant que pour l'architecte d'une maison, que cette "mise en forme" procède uniquement par les seules relations de causes à effets ; comme si on voulait [les matérialistes] placer une porte, puis un mur, puis un plafond, etc., sans avoir au préalable une vue globale sur l'immeuble qu'on veut construire. Il faut d'abord que l'objet soit pensé dans son ensemble, puis, en affiner les mécanismes, puis les associer, et enfin les faire marcher ensemble, le tout dans une relative harmonie. Le cheminement de la logique fait le chemin inverse, et essaie finalement de "déduire" par tâtonnements une forme globale de l'univers et de la vérité, en partant de chaînes de conséquences.
C'est pourquoi il est vain de vouloir décrire la réalité, ou la vérité, par la seule association des effets constatés de cette même réalité ou vérité. Il admet que certaines actions sans contact peuvent être des actions avec contact encore ignorées, telles que la télépathie, mais explique mieux son idée avec l'exemple de la satisfaction de réussir quelque chose après de nombreux essais infructueux, pour exprimer l'idée d'action sans contact. Ainsi, les erreurs passées agissent sur les succès futurs.
Cela permet d'introduire le principe d'émergence, puisqu'elle ne dépend pas uniquement des facteurs connus de façon fiable, mais aussi d'une "somme harmonique imprévisible" de facteurs connus, et inconnus.
Ce qui est intéressant pour nous ici est que nous avons pu scinder deux champs complets de la logique, celle qui est matérialiste et déterministe, et celle qui est indéterministe ou quantique, et de dire que "la réalité", c'est les deux à la fois.
Gaïa
Dès l'antiquité (on aime bien dans cet article repartir de zéro) on nomma "logos", la raison, l'acte qui consiste à ordonner les événements en allant des causes vers les effets.
Kepler fut le premier à assimiler la Terre à un organisme "rond et unique", bien qu'auparavant De Vinci avait fait l'analogie entre le Terre et les mécanismes du corps. Henry-David Thoreau voyait la Terre comme une créature à part entière qui possède un esprit. Huxley observe qu'elle est même capable de s'auto-réguler, et Lovelock a la sensation que les humains et la Terre vivent en co-évolution.
Vernadsky énonce le premier le concept de "biosphère", qui est un ensemble qui inclue l'atmosphère et la lithosphère, régie par les lois physiques. Cela amène Walter Canon à constater l'existence de processus homéostasiques et à introduire le concept de "Gaïa".
Pour Teilhard de Chardin, "matière et esprit sont les deux facettes d'une même pièce". Il conçoit la cosmogénèse comme un processus dynamique, ce qui ne va pas pour plaire à l'église catholique pour qui tout est statique, comme dans leur tête. Il invoque la place du hasard dans l'évolution, ainsi qu'évidemment, un plan divin, ce qui est contradictoire avec le hasard. De fait, il conçoit la création comme un acte libre.
Il représente le point Oméga comme le lieu de la convergence évolutive où se produit l'harmonisation de toutes les consciences, et introduit ainsi le concept de Noosphère, du grec "Noos", esprit, en référence à la biosphère et probablement la technosphère.
Gaïa, le système-Terre, serait un organisme global animé et actif, où c'est le milieu qui modifie les espèces et non l'inverse. Dans cette perception, on abouti au terme bien connu selon lequel "le tout est plus que la somme des parties".
Tout ceci nous rappelle que la logique n'a pas encore résolu les principales énigmes philosophiques, et pourtant, que ce n'est que par elle qu'elles peuvent l'être. Dès lors, il est temps d'introduire des concepts nouveaux, tels que la logique tétravalente, capable de soutenir des explications qui rendent logique qu'à la fois, le hasard et la liberté font partie d'un processus universel... qui n'est d'ailleurs que "statistiquement" déterministe.
La place de la logique tétravalente
Logique tétravalente s'inscrire dans la continuité des logiques multivalentes, dans la mesure où elle ne s'embarrasse pas du tiers-exclu. Il nous semble prometteur que certaines logiques fassent appel à la théorie des graphes, car cela nous servira de point de départ.
La logique tétravalente s'exprime par un arbre nodal qu'il faut parcourir pour aller de la proposition à la démonstration. Quand l'ensemble des prédicats de la proposition aboutissent à des conclusions, alors la proposition est démontrée. En ce sens, elle fonctionne "de proche en proche", comme la pensée, et c'est une "action par contact". Elle est donc matérialiste, principalement.
Mais l'intérêt de la logique tétravalente réside dans la non-exclusion explicite du terme-tiers, ce qui va contrarier beaucoup de logiciens qui considèrent l'univers comme une machine de Turing, dans laquelle tout peut être démontré (ce qui est un prédicat des la logique classique). Pourtant, l'intérêt de la logique tétravalente sera de pouvoir démontrer qu'une proposition puisse être indémontrable (ce qui est un prédicat de l'indécidabilité).
La logique classique relève du déterminisme, et, sans l'avoir précisément établi comme tel, alors que c'est pourtant le cas, ne concerne que les faits dits macroscopiques. En réalité toutes les mathématiques sont macroscopiques. C'est en cela que la logique tétravalente se distingue de tout ce paquet de logiques, dès lors qu'elle s'autorise à devenir indéterministe, ce qui s'exprime de façon logicielle par le fait de ne pas s'exécuter dans un ordre pré-établi.
Pour donner un exemple trivial de cette explication, revenons brièvement sur le nombre Pi, qui s'obtient par la formule :
π = 4 - 4/3 + 4/5 - 4/7 + 4/9 - 4/11...
Phi, lui, s'obtient par la formule :
φ = 4 - 4/3 - 4/7 - 4/11 -4/19... (ou par "ma" formule φ=1+1/φ, mais bon...).
Note de Norman : (perso, je préfère la formule φ²=φ+1 d'où je déduis φ=φ²-1 que je réduis à φ=(φ+1)(φ-1) qu'on peut calculer itérativement)
En réalité on peut obtenir n'importe quelle valeur de l'univers si on change seulement l'ordre des termes de la suite, de même qu'on peut changer le sens d'une phrase en permutant des mots. C'est à dire que le déterminisme tient au fait que les calculs soient toujours faits dans le même ordre. En LT, des données peuvent être en attente, et intervenir ultérieurement, ce que fait le terme tiers. De même, elles peuvent relever de la conscience, ce que fait le terme médian.
Cela, Brouwer (l'auteur de la LI) l'avait très bien pressenti en discriminant le fait que la logique classique s'embarrasse de l'infini et du tiers-exclu, là où la logique intuitionniste se contente de nombres finis et n'exclue aucune limitation arbitraire. Il semble donc que le problème des solutions indéterministes soient lié aux infinis. Qu'est-ce que l'infini, sinon une construction de l'esprit, et même : une illusion ? (On développera ceci dans la partie réservée aux hypothèses).
La logique tétravalente sera appropriée pour les calculs complexes dans lesquels peuvent intervenir des facteurs aléatoires, tels que l'indéterminisme quantique, et donc, ce qui en découle logiquement : la liberté. La logique déterministe, elle, doit se forcer à éluder toute notion aléatoire pour prétendre à une quelconque véracité "idéalisée et statique".
Note en passant (on vous la ressort souvent mais cela ne fait pas de mal) : les calculs économiques sont fondés sur des processus déterministes, et pour qu'ils soient viables, il faut absolument brimer au maximum la liberté des humains. C'est pour cette raison principalement (et non pour la santé des gens) que la vitesse sur autoroute est souvent baissée, que les dictatures sont florissantes, et que la pauvreté instaurée arrive à être "profitable". Le potentiel de la logique tétravalente n'est pas moins que de permettre de concevoir un système social qui brime le moins possible de liberté.
Note importante : Dans la cosmogonie Oummaine, la liberté, fruit de l'indéterminisme quantique, bien que non-fruit du hasard (ce qui est une contradiction possible à résoudre par la définition des axiomes) est centrale dans le fonctionnement de l'univers. L'âme individuelle (chez les humains seulement) et l'âme collective (pour tout le vivant) agissent sur des processus quantiques, en rompant leur indéterminisme, de sorte à engendrer une cascade de conséquences chimiques qui peuvent être responsables des mutations génétiques jugées profitables et harmoniques, aussi bien qu'à l'occasion d'un choix libre, ou encore de la télépathie. C'est de cette manière que les lois morales sont rendues effectives. Ainsi, ceux qui croient à "l'univers est une machine de Turing", oublient seulement l'existence des lois morales.
Il faut comprendre que les groupes macroscopiques ne sont pas situés "au-dessus" des groupes microphysiques, et donc ne peuvent les inclure, comme on ne peut déduire que pour résoudre un groupe macroscopique, il faudrait d'abord résoudre les groupes microscopiques qui en font partie (faisant du premier une dépendance du second). De fait, les groupes macroscopiques sont en réalité une réduction psychologique d'une réalité globale qui elle, est microscopique.
Par exemple l'agitation des atomes dans un bol est imprévisible, mais statistiquement il s'en dégage des données macroscopiques stables, telles que la pression et la température. Mais ces données macroscopiques n'ont de valeur, et d'existence, que pour un entendement produit par une activité cérébrale.
L'indéterminisme dont tient compte la logique tétravalente est aussi l'occasion d'interroger les fondements de la raison, des processus intellectuels et des capacités cognitives. Ainsi une bonne part des solutions dépendra de l'entendement, ce qui sera l'occasion de réaliser que quasiment tout ce qu'on croit réel n'existe peut-être en réalité que dans notre entendement. C'est une perspective assez vertigineuse.
Cela veut dire qu'on sait d'avance que pour être opérationnelle, la logique tétravalente devra partir de postulats définis par avance comme étant arbitrairement considérés comme vrais, mais potentiellement réfutables.
Enfin, la logique tétravalente est aussi un moyen d'intégrer des calculs de prédiction qui peuvent devoir s'affiner avec le temps, ou qui doivent tenir compte de ces calculs eux-mêmes. Ainsi dans l'exemple d'une éruption volcanique (qui est une émergence) le calcul récursif n'aura de cesse de s'actualiser, et de s'affiner, jusqu'à correspondre avec la réalité de l'événement.
La réponse que renvoie un calcul tétravalent, semble être un degré de validité estimé suffisant de la réponse à la question "Quand aura lieu l'éruption volcanique". Et, comme on se l'imagine, l'ordinateur n'aura de cesse de poser des questions pour pouvoir affiner ses modèles. Il pourra même s'orienter vers les questions les plus pertinentes.
Car après tout, ce qui est véritablement prometteur dans cette forme de logique propositionnelle, c'est non seulement qu'elle est indéterministe, mais surtout que, à cause ou grâce à cela, elle est essentiellement activable par des ordres donnés à l'oral. On l'imagine bien poser des questions pertinentes pour l'aider à résoudre les problèmes qui lui sont soumis.
*
Lexique
Axiome : principe servant de base à une démonstration, évident en soi
Postulat : Proposition que l'on demande d'admettre
Prédicat : élément autour duquel s'organise la fonction qui permet la réponse ; c'est un syntagme verbal et non nominal.
Syntagme : constituant syntaxique et sémantique de la phrase
Ontologie : (philosophie) interrogation du sens d'un mot
Epistémologie : étude critique de la science / des connaissances
Heuristique : art d'inventer et de faire des découvertes, par construction d'une vraisemblance, au moyen d'essais et d'erreurs.
Symboles
| col2 | col3 | |
|---|---|---|
| | | tel que | algèbre |
| ∆ | incrément (delta) | algèbre |
| ∼ | équivalence | algèbre |
| ≈ | approximation | algèbre |
| ≃ | équivalence d'homotopie | algèbre |
| ≅ | isomorphisme | algèbre |
| ≡ | congruence, égalité définitionnelle | algèbre |
| = | égalité propositionnelle | algèbre |
| → | s'applique tel que | algèbre |
| ⟼ | s'applique | lambda-calcul |
| ⟹ | implication logique | ensembles |
| ⟺ | équivalence logique | ensembles |
| ∀ | tout | ensembles |
| ∃ | existence | ensembles |
| ∄ | non-existence | ensembles |
| ∈ | appartient à, est compris dans | ensembles |
| ∉ | n'appartient pas, n'est pas compris dans | ensembles |
| ∋ | contient, comprend | ensembles |
| ∌ | ne contient pas, ne comprend pas | ensembles |
| ⋂ | intersection | ensembles |
| ⋃ | union | ensembles |
| ⊂ | est un sous-ensemble de ; implication réciproque (suppose qu'il reste un objet hors de l'inclusion) | ensembles |
| ⊃ | contient le sous-ensemble, implication (suppose qu'il reste un objet hors de l'inclusion) | ensembles |
| ⋀ | conjonction (AND) | ensembles |
| ⋁ | disjonction (OR) | ensembles |
| ⊼ | nand (not-and) | ensembles |
| ⊽ | nor (or exclusif) | ensembles |
| ¬ | la négation, n'est pas | logiques |
| ⊤ | tautologie (vrai) | logiques |
| ⊥ | contradiction (faux) | logiques |
| ⊢ | démontre que | logiques |
| ⊬ | ne démontre pas | logiques |
| ⊧ | il existe des modèles pour | logiques |
| ⊨ | conséquence logique | logiques |
| ∥ | ou (booléen) | informatique |
| && | et (booléen) | informatique |
| ↠ | surjection | algèbre |
| ↬ | immersion | algèbre |
| ↦ | devient (algo) | lambda-calcul |
| ⩴ | affectation (2x deux points-égal) | logique modale |
| ☐ | nécessité logique | logique modale |
| ⏹ | Cqfd | logique modale |
| ◊ | possibilité logique | logique modale |
| ∴ | par conséquent (donc) | logique modale |
| ∵ | parce que (cause) | logique modale |
| ∼ | négation logique | logique linéaire |
| ⊸ | devient (consommation des prédicats) = négation linéaire + disjonction multiplicative | logique linéaire |
| ≔ | est défini comme | logique linéaire |
| ≡ | équivalence linéaire (permet de joindre la LC et la LI) | logique linéaire |
| ⊙ | négation de disjonction exclusive | logique linéaire |
| ⊕ | disjonction additive (tenseur, ≈ "ou") | logique linéaire |
| ⊗ | conjonction (tenseur, ≈ "et") | logique linéaire |
| ⅋ | disjonction exclusive (non-et ≈ "ou") | logique linéaire |
| ⋉ | produit semi-direct | logique linéaire |
| ⋊ | produit semi-direct | logique linéaire |
| ! | factorielle (nombres réels possiblement infinis, distingués des valeurs logiques) | logique linéaire |
| フ | "fu" (objectif) | logique linéaire |
| ヲ | "wo" (subjectif) | logique linéaire |
Plus d'infos sur les connecteurs logiques. Ils sont nombreux et cela, ce n'est que pour la logique divalente...
Citation de Edgar Morin
L'abstraction formalisatrice a fini par se prendre pour la quintessence de la réalité alors qu'elle en est la déshydratation."
Merci à Norman Molhant pour sa relecture corrective très précise et judicieuse.